I was never interested in mathematics at school, perhaps because of the way it was taught; it was seen as a subject for boys in the 50s. Today, things may have changed a bit. In any case, from early on, I was on the creative spectrum, rather than the logical/rational one. Was this a result of nature or nurture? Perhaps a little of both.
Today, however, I’m fascinated by the idea of The Golden Ratio, and its links with mathematics, nature and art. In fact, it also has links with science, architecture, music, and many other areas besides. The golden ratio essentially states that a + b is to a, as a is to b.
The Golden ratio is a special number (1.618), found by dividing a line into two parts, so that the longer part divided by the smaller part is also equal to the whole length divided by the longer part. It is often symbolized using phi, after the 21st letter of the Greek alphabet. In an equation form, it looks like this: a/b = (a+b)/a = 1.6180339887498948420
Around 1200, mathematician Leonardo Fibonacci discovered the unique properties of the Fibonacci Sequence. This sequence ties directly into the Golden ratio: if you take any two successive Fibonacci numbers, their ratio is very close to the Golden ratio. As the numbers get higher, the ratio becomes even closer to 1.618. For example, the ratio of 3 to 5 is 1.666. But the ratio of 13 to 21 is 1.625. Getting even higher, the ratio of 144 to 233 is 1.618. These numbers are all successive numbers in the Fibonacci sequence.
Here is a visual representation of a Fibonacci spiral which approximates the golden spiral, using Fibonacci sequence square sizes up to 34. Notice how the lengths get smaller in a spiral pattern.
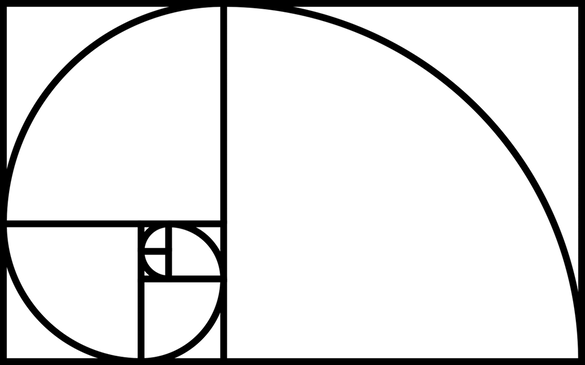
This spiral pattern is used throughout nature. Many shells, including snail shells and nautilus shells, are perfect examples of the Golden spiral.
The seeds of a sunflower, which start in the centre and radiate outwards to fill the space, repeated endlessly, are a perfect example of the Golden Ratio in nature. There are no gaps from beginning to end. Some spiders form their webs in spirals that suggest the repetitive pattern of the golden spiral. And the beautiful designs on the wings of moths and butterflies approximate the golden mean. Similarly, hurricanes often portray the golden spiral. Other examples are roses, spiral galaxies, such as The Milky Way, dolphins, starfish, sea urchins, ants, cauliflowers and honeybees, which all exhibit the fibonacci proportion.
The symbol that has come to represent this ratio is the 21st letter of the Greek alphabet phi.
Leonardo of Pisa, also known as Leonardo Pisano or Fibonacci, was an Italian mathematician, born in Pisa about 1175 AD.Fibonacci popularized the Hindu-Arabic numeral system in the Western World through his Book of Calculation in 1202. In the same publication, he introduced the sequence of Fibonacci numbers to Europe.
Scientists today, have moved away from thinking about such considerations, as they are deemed to belong to an ancient time. Darwinian evolutionary theories, and findings from archaeological diggings are more likely to be of interest to the modern mind, because they are evidence-based.
It still amazes me to see how much order, beauty and patterning exist in the natural world around us. I wonder at the time it took, and the processes at work, to create all of this amazing diversity surrounding us, and of which we are a part.
Thanks for this.
I love this piece. I fell in love with maths when I realised it’s not just about numbers. S
Thanks sooo much, coz my big brother hates it… I love your brilliant piece about a sister keeping in touch with a dead brother! Am following.
That’s right, me too. Only recently!
Well Anne, let me start by stating I AM no mathematician but that I AM fascinated by things strangely mathematical. This article is in a field covering that fascination. Oh the beauty of nature and the power of the human mind to discover and explore these phenomena. I LOVE this post. More please.
That’s great, coz I wanted to follow up on art and the GR. You’re always such a big help,IH.
Hi Marcia
Thanks for finding me.
I looked at your excellent blog post also.
Keep in touch
Anne
Thanks for finding me, Marcia.
Will look at your blog post.
Anne
Thanks for finding me!